Materi matematika hiperbola akan mengungkap bentuk dan sifat kurva unik ini. Hiperbola, sebagai salah satu irisan kerucut, memiliki karakteristik yang menarik dan beragam penerapannya dalam berbagai bidang. Mari kita telusuri definisi, jenis, unsur-unsur, persamaan, sifat-sifat, dan penerapannya dalam kehidupan sehari-hari.
Materi ini akan membahas secara detail tentang hiperbola, mulai dari pengertian dasar hingga contoh penerapannya. Kita akan mempelajari berbagai bentuk persamaan hiperbola, jenis-jenisnya, dan unsur-unsur penting seperti titik fokus, titik puncak, sumbu utama, dan asimtot. Diskusi akan dilengkapi dengan ilustrasi gambar dan contoh soal, sehingga pemahaman Anda akan semakin komprehensif.
Definisi dan Pengertian Hiperbola
Hiperbola merupakan salah satu jenis kurva konik yang memiliki dua cabang terpisah. Konsep hiperbola penting dalam berbagai bidang matematika dan ilmu pengetahuan, seperti dalam navigasi dan astronomi.
Definisi Matematika Hiperbola
Hiperbola didefinisikan sebagai tempat kedudukan titik-titik yang selisih jaraknya terhadap dua titik fokus tetap (yang disebut titik fokus) selalu konstan.
Bentuk Persamaan Hiperbola
Hiperbola memiliki beragam bentuk persamaan, tergantung pada posisi sumbu utama (sumbu yang menghubungkan kedua titik fokus). Berikut beberapa bentuk persamaan hiperbola yang umum ditemui:
- Persamaan Standar Hiperbola dengan Sumbu Utama Horizontal: (x-h)²/a²
-(y-k)²/b² = 1. Dimana (h,k) adalah koordinat pusat hiperbola, a adalah setengah jarak antara titik puncak, dan b terkait dengan bentuk dan ukuran hiperbola. - Persamaan Standar Hiperbola dengan Sumbu Utama Vertikal: (y-k)²/a²
-(x-h)²/b² = 1. Sama seperti di atas, (h,k) adalah koordinat pusat hiperbola, a adalah setengah jarak antara titik puncak, dan b terkait dengan bentuk dan ukuran hiperbola. - Persamaan Umum Hiperbola: Ax² + Cy² + Dx + Ey + F = 0. Persamaan ini dapat merepresentasikan berbagai bentuk hiperbola, namun untuk menentukan bentuknya diperlukan analisis lebih lanjut.
Perbandingan Persamaan Hiperbola
| Karakteristik | Sumbu Utama Horizontal | Sumbu Utama Vertikal |
|---|---|---|
| Persamaan Standar | (x-h)²/a²
|
(y-k)²/a²
|
| Letak Titik Puncak | Pada sumbu x | Pada sumbu y |
| Arah Cabang | Membuka ke kanan dan kiri | Membuka ke atas dan bawah |
| Koordinat Titik Fokus | (h±c, k) | (h, k±c) |
Catatan: c² = a² + b² merupakan hubungan penting dalam menentukan koordinat titik fokus hiperbola.
Jenis-jenis Hiperbola
Setelah memahami dasar-dasar hiperbola, kita akan mempelajari berbagai jenisnya. Memahami perbedaan jenis hiperbola sangat penting untuk mengidentifikasi dan menganalisis bentuknya dalam berbagai konteks matematika.
Identifikasi Jenis-jenis Hiperbola
Hiperbola dapat dikategorikan berdasarkan posisi sumbu utamanya. Posisi sumbu utama ini menentukan orientasi dan bentuk grafik hiperbola.
Hiperbola dengan Sumbu Utama Sejajar Sumbu-x
Jenis hiperbola ini memiliki persamaan umum yang berbentuk (x-h)²/a²
-(y-k)²/b² = 1 atau (y-k)²/a²
-(x-h)²/b² = 1. Parameter ‘a’ dan ‘b’ memengaruhi bentuk dan ukuran hiperbola.
- Jika persamaan berbentuk (x-h)²/a²
-(y-k)²/b² = 1, sumbu utama hiperbola sejajar dengan sumbu-x, dan titik fokusnya terletak pada sumbu-x. Grafiknya membuka ke kanan dan kiri. - Jika persamaan berbentuk (y-k)²/a²
-(x-h)²/b² = 1, sumbu utama hiperbola sejajar dengan sumbu-y, dan titik fokusnya terletak pada sumbu-y. Grafiknya membuka ke atas dan bawah.
Contoh Grafik
Untuk lebih memahami, berikut adalah contoh grafik dari kedua jenis hiperbola tersebut. Perhatikan bagaimana bentuk dan orientasi grafik berubah berdasarkan persamaan yang digunakan.
- Grafik hiperbola (x-2)²/9 – (y+1)²/4 = 1 adalah hiperbola dengan sumbu utama sejajar sumbu-x, yang membuka ke kanan dan kiri. Pusat hiperbola berada di (2,-1). Nilai a=3 dan b=2, yang akan menentukan ukuran dan bentuk hiperbola.
- Grafik hiperbola (y-3)²/16 – (x+1)²/25 = 1 adalah hiperbola dengan sumbu utama sejajar sumbu-y, yang membuka ke atas dan bawah. Pusat hiperbola berada di (-1,3). Nilai a=4 dan b=5, yang akan menentukan ukuran dan bentuk hiperbola.
Perbedaan Karakteristik
Berikut ringkasan perbedaan karakteristik hiperbola berdasarkan posisi sumbu utama:
| Karakteristik | Hiperbola dengan Sumbu Utama Sejajar Sumbu-x | Hiperbola dengan Sumbu Utama Sejajar Sumbu-y |
|---|---|---|
| Persamaan Umum | (x-h)²/a²
|
(y-k)²/a²
|
| Sumbu Utama | Sejajar sumbu-x | Sejajar sumbu-y |
| Fokus | Terletak pada sumbu-x | Terletak pada sumbu-y |
| Bentuk Grafik | Membuka ke kanan dan kiri | Membuka ke atas dan bawah |
Unsur-unsur Hiperbola: Materi Matematika Hiperbola
Setelah memahami konsep dasar hiperbola, mari kita telusuri unsur-unsur pentingnya. Pemahaman terhadap unsur-unsur ini akan mempermudah dalam menganalisis dan menggambarkan bentuk hiperbola.
Titik Fokus dan Titik Puncak
Titik fokus pada hiperbola merupakan dua titik yang berperan penting dalam menentukan bentuknya. Kedua titik ini terletak di sepanjang sumbu utama dan berjarak sama dari pusat hiperbola. Titik puncak adalah titik-titik di mana kurva hiperbola memotong sumbu utama. Posisi titik puncak dan titik fokus saling terkait erat dalam menentukan bentuk keseluruhan hiperbola.
-
Titik fokus terletak di sepanjang sumbu utama hiperbola, berjarak sama dari pusat.
-
Titik puncak adalah titik potong hiperbola dengan sumbu utama. Ada dua titik puncak pada hiperbola.
-
Jarak antara titik fokus ke pusat sama dengan jarak titik puncak ke pusat.
Sumbu Utama
Sumbu utama hiperbola merupakan garis lurus yang melalui kedua titik fokus dan titik puncak. Panjang sumbu utama memengaruhi ukuran keseluruhan hiperbola. Sumbu utama ini merupakan garis referensi penting dalam menentukan posisi titik-titik lain pada hiperbola.
Perhatikan bahwa sumbu utama merupakan sumbu simetri untuk hiperbola.
Asimtot
Garis asimtot adalah garis lurus yang mendekati kurva hiperbola tanpa pernah menyentuhnya. Asimtot memberikan gambaran tentang perilaku kurva hiperbola pada nilai x dan y yang besar. Asimtot sangat membantu dalam menggambar sketsa hiperbola.
-
Asimtot adalah garis lurus yang mendekati kurva hiperbola pada nilai x dan y yang besar.
-
Asimtot memberikan gambaran tentang bentuk dan perilaku hiperbola pada daerah yang jauh dari pusat.
-
Asimtot membantu dalam menggambar sketsa hiperbola dengan lebih akurat.
Menentukan Koordinat Titik Fokus dan Titik Puncak
Koordinat titik fokus dan titik puncak hiperbola dapat ditentukan dengan menggunakan persamaan hiperbola dan parameter-parameter yang diketahui, seperti panjang sumbu semi-mayor dan semi-minor, serta posisi pusat hiperbola. Rumus-rumus ini memungkinkan kita untuk menghitung koordinat-koordinat tersebut secara tepat.
Rumus umum untuk menentukan koordinat titik fokus dan titik puncak bergantung pada bentuk persamaan hiperbola (horizontal atau vertikal). Konsep dasar geometri dan aljabar akan membantu dalam proses perhitungan.
Contohnya, jika diketahui persamaan hiperbola dalam bentuk standar dan nilai parameternya, kita dapat menentukan koordinat titik fokus dan titik puncak dengan mengaplikasikan rumus yang sesuai. Misalnya, pada hiperbola dengan sumbu utama horizontal, koordinat titik fokus dan puncak dapat ditentukan dengan rumus yang melibatkan a, b, dan c (dimana c 2 = a 2 + b 2). Untuk hiperbola vertikal, rumusnya sedikit berbeda.
Persamaan Hiperbola
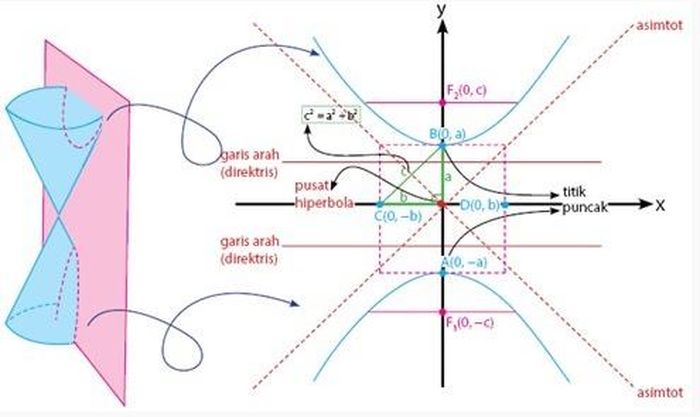
Dalam mempelajari hiperbola, memahami persamaannya merupakan langkah krusial. Persamaan hiperbola memungkinkan kita untuk menggambarkan bentuk dan posisi hiperbola dalam sistem koordinat. Mengetahui cara menentukan persamaan hiperbola dari data yang diberikan, seperti titik fokus dan titik puncak, sangat penting untuk berbagai aplikasi matematika dan sains.
Menentukan Persamaan Hiperbola dari Titik Fokus dan Titik Puncak
Untuk menentukan persamaan hiperbola, kita perlu mengetahui koordinat titik fokus dan titik puncaknya. Langkah-langkah berikut menjelaskan prosesnya secara sistematis:
- Identifikasi posisi sumbu utama hiperbola. Jika titik puncak berada pada sumbu x, maka persamaan hiperbola berpusat di (h, k) akan berbentuk
(x-h)2/a 2
(y-k)2/b 2 = 1
Jika titik puncak berada pada sumbu y, maka persamaan hiperbola berpusat di (h, k) akan berbentuk
(y-k)2/a 2
(x-h)2/b 2 = 1
- Tentukan koordinat titik pusat (h, k) hiperbola. Titik pusat berada tepat di tengah-tengah antara kedua titik puncak.
- Hitung nilai a, jarak antara titik pusat dan titik puncak. Nilai a merupakan setengah dari jarak antara kedua titik puncak.
- Hitung nilai c, jarak antara titik pusat dan titik fokus. Nilai c merupakan setengah dari jarak antara kedua titik fokus.
- Gunakan hubungan c 2 = a 2 + b 2 untuk menghitung nilai b.
- Substitusikan nilai h, k, a, dan b ke dalam persamaan hiperbola yang sesuai (berdasarkan sumbu utama hiperbola) untuk mendapatkan persamaan hiperbola yang dicari.
Menyelesaikan Soal Perhitungan Persamaan Hiperbola
Berikut contoh penerapan langkah-langkah tersebut:
Contoh Soal: Tentukan persamaan hiperbola jika diketahui titik puncaknya di (3, 2) dan (3, -2) serta titik fokusnya di (3, 4) dan (3, -4).
- Sumbu utama hiperbola berada pada sumbu y, karena titik puncak dan titik fokus berada pada sumbu y.
- Titik pusat (h, k) adalah (3, 0).
- a = 2 (jarak antara titik pusat dan titik puncak)
- c = 4 (jarak antara titik pusat dan titik fokus)
- b2 = c 2
a2 = 16 – 4 = 12
- Persamaan hiperbola adalah (y-0) 2/4 – (x-3) 2/12 = 1
Menentukan Persamaan Asimtot Hiperbola
Asimtot hiperbola merupakan garis lurus yang mendekati kurva hiperbola tanpa pernah menyentuhnya. Persamaan asimtot hiperbola sangat membantu dalam menggambar grafik hiperbola.
- Jika sumbu utama pada sumbu x, maka persamaan asimtotnya adalah:
y – k = ±(b/a)(x – h)
- Jika sumbu utama pada sumbu y, maka persamaan asimtotnya adalah:
y – k = ±(a/b)(x – h)
Dengan mengetahui nilai a, b, h, dan k, persamaan asimtot dapat langsung ditentukan.
Sifat-sifat Hiperbola
Hiperbola, sebagai salah satu jenis kurva konik, memiliki sifat-sifat unik yang membedakannya dari kurva lainnya seperti parabola dan elips. Sifat-sifat ini memengaruhi bentuk dan posisi grafik hiperbola di bidang koordinat.
Perbedaan dengan Kurva Lain
Hiperbola berbeda dari parabola dan elips dalam hal bentuk dan karakteristik titik-titik pada kurvanya. Perbedaan mendasarnya terletak pada sifat asimtotnya, dan cara titik-titik pada kurva mendekati garis asimtot tersebut. Parabola hanya memiliki satu titik fokus, sementara hiperbola memiliki dua titik fokus. Hal ini berpengaruh langsung pada bentuk grafik hiperbola yang cenderung memanjang ke arah dua sumbu yang berlawanan.
Sifat-sifat yang Memengaruhi Bentuk dan Posisi Grafik
Beberapa sifat hiperbola yang memengaruhi bentuk dan posisi grafiknya antara lain:
- Asimtot: Garis asimtot merupakan garis lurus yang didekati oleh kurva hiperbola, tetapi tidak pernah dipotongnya. Asimtot berperan penting dalam menentukan bentuk dan arah perpanjangan kurva. Kemiringan dan posisi asimtot menentukan orientasi dan bentuk hiperbola. Asimtot dapat digunakan untuk sketsa grafik hiperbola dengan cepat.
- Titik Fokus: Dua titik fokus hiperbola menentukan bentuk dan ukuran kurva. Jarak antara titik-titik fokus memengaruhi eksentrisitas hiperbola, yang pada akhirnya memengaruhi seberapa “memanjang” bentuknya. Letak titik fokus pada sumbu-sumbu koordinat menentukan orientasi hiperbola pada bidang koordinat.
- Sumbu Utama dan Sumbu Minor: Panjang sumbu utama dan sumbu minor menentukan ukuran hiperbola. Perbandingan panjang sumbu-sumbu ini memengaruhi eksentrisitas dan bentuk hiperbola. Sumbu-sumbu ini juga menentukan posisi titik-titik fokus.
- Eksentrisitas: Eksentrisitas hiperbola, yang didefinisikan sebagai rasio jarak fokus ke jarak dari pusat ke sumbu, menentukan seberapa memanjang kurva. Semakin besar eksentrisitas, semakin memanjang hiperbola. Eksentrisitas ini terkait langsung dengan kemiringan asimtot.
Ringkasan Sifat-sifat Hiperbola
| Sifat | Penjelasan |
|---|---|
| Asimtot | Garis lurus yang didekati oleh kurva, tetapi tidak pernah dipotong. |
| Titik Fokus | Dua titik yang menentukan bentuk dan ukuran hiperbola. |
| Sumbu Utama/Minor | Menentukan ukuran dan orientasi hiperbola. |
| Eksentrisitas | Rasio jarak fokus ke jarak dari pusat ke sumbu, menentukan seberapa memanjang hiperbola. |
Penerapan Hiperbola dalam Kehidupan Sehari-hari
Hiperbola, meskipun tampak sebagai konsep matematika abstrak, memiliki aplikasi yang menarik dalam berbagai bidang kehidupan sehari-hari. Dari sistem navigasi hingga teknik rekayasa, hiperbola berperan penting dalam memecahkan masalah dan meningkatkan efisiensi.
Penerapan dalam Sistem Navigasi GPS
Sistem navigasi GPS memanfaatkan konsep hiperbola untuk menentukan posisi suatu titik. Satelit GPS memancarkan sinyal radio yang diterima oleh penerima GPS di bumi. Perbedaan waktu tempuh sinyal dari beberapa satelit digunakan untuk menentukan jarak penerima ke satelit-satelit tersebut. Dari jarak-jarak ini, sistem GPS dapat menghitung posisi penerima di bumi dengan presisi tinggi. Proses ini secara matematis melibatkan persamaan hiperbola, di mana setiap satelit membentuk satu cabang hiperbola yang melalui posisi penerima.
Penerapan dalam Teknik Rekayasa, Materi matematika hiperbola
Dalam teknik rekayasa, khususnya dalam perancangan struktur, hiperbola seringkali ditemukan dalam bentuk lengkungan yang memberikan kekuatan dan stabilitas yang optimal. Contohnya, lengkungan hiperbola dapat ditemukan pada jembatan gantung tertentu, atau pada desain tertentu untuk mendistribusikan beban secara efektif. Bentuk hiperbola pada struktur ini membantu menopang beban yang lebih besar dengan material yang lebih sedikit, mengoptimalkan efisiensi dan kekuatan.
Penerapan dalam Fisika
Konsep hiperbola juga berperan dalam beberapa fenomena fisika. Salah satunya adalah dalam analisis lintasan benda yang bergerak dengan percepatan konstan, seperti peluru yang ditembakkan. Bentuk lintasan yang dihasilkan terkadang dapat didekati dengan hiperbola, tergantung pada sudut dan kecepatan peluru. Perhitungan lintasan ini menggunakan prinsip-prinsip fisika klasik dan melibatkan persamaan hiperbola dalam perhitungannya.
Contoh Penerapan Hiperbola
- Sistem Navigasi GPS: Perbedaan waktu tempuh sinyal radio dari beberapa satelit GPS digunakan untuk menentukan posisi penerima di bumi. Perhitungan ini memanfaatkan sifat-sifat hiperbola untuk menghitung jarak penerima ke satelit-satelit tersebut.
- Teknik Rekayasa: Bentuk lengkungan hiperbola dapat ditemukan pada beberapa jenis jembatan gantung, yang dirancang untuk mendistribusikan beban secara efektif. Bentuk hiperbola pada struktur ini membantu menopang beban yang lebih besar dengan material yang lebih sedikit.
- Fisika: Lintasan peluru yang ditembakkan dengan sudut tertentu dapat didekati dengan bentuk hiperbola, meskipun dalam kenyataannya, lintasan peluru lebih tepatnya parabola.
Penerapan hiperbola dalam kehidupan sehari-hari sangat beragam, dari sistem navigasi hingga teknik rekayasa dan fisika. Konsep ini membantu dalam menyelesaikan berbagai permasalahan yang membutuhkan perhitungan dan analisis yang tepat.
Soal dan Latihan Hiperbola
Berikut disajikan beberapa soal latihan untuk mengasah pemahaman Anda tentang hiperbola. Soal-soal ini dirancang dengan tingkat kesulitan yang bervariasi, mulai dari yang sederhana hingga yang lebih kompleks. Solusi dan penjelasan untuk setiap soal disertakan untuk membantu Anda memahami konsep dengan lebih baik.
Contoh Soal Latihan Hiperbola
Berikut ini lima soal latihan hiperbola dengan tingkat kesulitan yang berbeda-beda. Setiap soal dilengkapi dengan solusi dan penjelasan untuk membantu Anda dalam memahami konsep hiperbola dengan lebih baik.
| Soal | Solusi dan Penjelasan |
|---|---|
| 1. Tentukan persamaan hiperbola dengan titik fokus di (0, 3) dan (0, -3), dan sumbu minor sepanjang 4. | Persamaan hiperbola dengan titik fokus (0, ±c) dan sumbu minor 2b adalah (y2/a2)
Diketahui c = 3 dan 2b = 4, sehingga b = 2. |
| 2. Tentukan titik puncak dan titik fokus dari hiperbola dengan persamaan 9y2 – 16x 2 = 144. | Ubah persamaan menjadi bentuk baku: (y 2/16)
Dari persamaan ini, a 2 = 16 dan b 2 = 9. Titik fokusnya adalah (0, ±c) = (0, ±5). |
| 3. Jika sebuah hiperbola memiliki persamaan (x-2)2/9 – (y+1) 2/4 = 1, tentukan pusat, titik puncak, dan titik fokusnya. | Pusat hiperbola adalah (h, k) = (2, -1). Titik puncaknya adalah (h ± a, k) = (2 ± 3, -1) = (5, -1) dan (-1, -1). Titik fokusnya adalah (h ± c, k) = (2 ± √13, -1). |
| 4. Sebuah hiperbola memiliki persamaan 4x29y 2 = 36. Tentukan persamaan asimtotnya. | Ubah persamaan ke bentuk baku: (x 2/9)
Persamaan asimtotnya adalah y = ±(b/a)x = ±(2/3)x |
| 5. Gambarkan sketsa hiperbola dengan persamaan x2/25 – y 2/16 = 1. | Sketsa hiperbola dengan sumbu utama sejajar sumbu-x, titik puncak di (±5, 0). |
Ringkasan Penutup

Melalui pembahasan ini, diharapkan Anda dapat memahami secara mendalam tentang materi matematika hiperbola. Dengan menguasai konsep dan sifat-sifat hiperbola, Anda akan mampu menyelesaikan berbagai soal dan mengaplikasikannya dalam konteks kehidupan nyata.
Semoga materi ini bermanfaat dalam perjalanan belajar matematika Anda.