Materi matematika regresi linear membahas tentang hubungan antara variabel-variabel, khususnya bagaimana satu variabel dipengaruhi oleh variabel lain. Metode ini sangat penting dalam berbagai bidang, dari ekonomi hingga ilmu sosial, untuk memahami pola-pola dan memprediksi tren. Memahami konsep dasar regresi linear, berbagai jenisnya, metode estimasi, interpretasi hasil, dan aplikasinya akan membuka wawasan baru dalam menganalisis data dan mengambil keputusan yang lebih baik.
Materi ini akan membahas definisi regresi linear, jenis-jenisnya seperti regresi linear sederhana dan berganda, metode estimasi parameter, interpretasi hasil regresi, dan penerapannya dalam berbagai bidang. Pembahasan akan dilengkapi dengan contoh kasus dan ilustrasi visual untuk mempermudah pemahaman. Selain itu, materi juga akan menjelaskan asumsi dan diagnostik yang perlu diperhatikan dalam model regresi linear untuk memastikan validitas dan keandalan hasil.
Definisi Regresi Linear

Regresi linear merupakan teknik statistik yang digunakan untuk memodelkan hubungan antara variabel dependen dan satu atau lebih variabel independen. Metode ini mengasumsikan hubungan linier antara variabel-variabel tersebut. Pemahaman akan regresi linear sangat penting dalam berbagai bidang, mulai dari bisnis hingga ilmu sosial, untuk memprediksi dan menganalisis data.
Definisi Matematika Regresi Linear
Regresi linear menggambarkan hubungan linier antara variabel dependen (Y) dan satu atau lebih variabel independen (X). Persamaan regresi linear sederhana dapat dituliskan sebagai: Y = a + bX + ε. Di mana:
- Y adalah variabel dependen.
- X adalah variabel independen.
- a adalah intercept (nilai Y ketika X = 0).
- b adalah koefisien regresi (kemiringan garis).
- ε adalah error term (kesalahan).
Tujuan utama regresi linear adalah untuk memperkirakan nilai a dan b yang terbaik untuk meminimalkan error term. Teknik ini biasanya menggunakan metode kuadrat terkecil (Ordinary Least Squares/OLS).
Konsep Dasar Regresi Linear
Konsep dasar regresi linear adalah untuk menemukan garis lurus yang terbaik menggambarkan hubungan antara variabel independen dan dependen. Garis ini berusaha untuk meminimalkan jarak antara titik-titik data dan garis itu sendiri. Hal ini penting untuk memprediksi nilai variabel dependen berdasarkan nilai variabel independen.
Ilustrasi Grafik Regresi Linear
Bayangkan grafik dengan sumbu X mewakili variabel independen (misalnya, jam belajar) dan sumbu Y mewakili variabel dependen (misalnya, nilai ujian). Garis regresi linear akan berupa garis lurus yang melewati titik-titik data dan menunjukkan hubungan antara jam belajar dan nilai ujian. Semakin dekat titik-titik data ke garis, semakin baik model regresi tersebut.
Hubungan Variabel Independen dan Dependen
Dalam konteks regresi linear, hubungan antara variabel independen dan dependen bersifat linier. Artinya, perubahan pada variabel independen akan menyebabkan perubahan proporsional pada variabel dependen. Misalnya, semakin banyak jam belajar, semakin tinggi nilai ujian yang diharapkan. Perlu diingat bahwa hubungan ini tidak selalu sempurna, dan terdapat faktor lain yang memengaruhi nilai variabel dependen.
Perbedaan Regresi Linear Sederhana dan Berganda
| Karakteristik | Regresi Linear Sederhana | Regresi Linear Berganda |
|---|---|---|
| Jumlah Variabel Independen | Satu | Dua atau lebih |
| Persamaan | Y = a + bX + ε | Y = a + b1X1 + b2X2 + … + ε |
| Interpretasi | Hubungan antara Y dan satu X | Hubungan antara Y dan beberapa X |
| Kompleksitas Model | Relatif sederhana | Lebih kompleks |
Jenis-jenis Regresi Linear: Materi Matematika Regresi Linear
Regresi linear merupakan teknik statistik yang digunakan untuk memodelkan hubungan antara variabel dependen dan satu atau lebih variabel independen. Jenis-jenis regresi linear yang berbeda menawarkan fleksibilitas dalam memodelkan hubungan yang kompleks. Pemahaman tentang berbagai jenis ini sangat penting untuk memilih model yang tepat untuk data dan tujuan analisis.
Regresi Linear Sederhana
Regresi linear sederhana melibatkan satu variabel independen dan satu variabel dependen. Model ini cocok untuk mengidentifikasi hubungan linear sederhana antara dua variabel. Misalnya, kita bisa menggunakan regresi linear sederhana untuk memprediksi harga rumah berdasarkan ukuran rumah. Dalam hal ini, ukuran rumah adalah variabel independen dan harga rumah adalah variabel dependen.
Contoh Kasus: Seorang peneliti ingin mengetahui hubungan antara jam belajar dan nilai ujian matematika. Ia mengumpulkan data dari beberapa siswa, dan variabel independen adalah jam belajar, sedangkan variabel dependen adalah nilai ujian matematika. Dengan regresi linear sederhana, ia dapat menentukan bagaimana jam belajar memengaruhi nilai ujian.
Regresi Linear Berganda
Regresi linear berganda melibatkan lebih dari satu variabel independen. Model ini memungkinkan kita untuk mengidentifikasi pengaruh masing-masing variabel independen terhadap variabel dependen, sambil mempertimbangkan pengaruh variabel lainnya. Misalnya, kita bisa menggunakan regresi linear berganda untuk memprediksi harga rumah berdasarkan ukuran rumah, lokasi, dan jumlah kamar tidur. Dalam hal ini, ukuran rumah, lokasi, dan jumlah kamar tidur adalah variabel independen, dan harga rumah adalah variabel dependen.
Contoh Kasus: Sebuah perusahaan ingin memprediksi penjualan produk berdasarkan harga produk, promosi yang dilakukan, dan pendapatan rata-rata konsumen. Dengan regresi linear berganda, perusahaan dapat menganalisis pengaruh masing-masing faktor terhadap penjualan.
Regresi Polinomial
Regresi polinomial adalah jenis regresi linear yang menggunakan polinomial untuk memodelkan hubungan antara variabel independen dan dependen. Model ini cocok untuk mengidentifikasi hubungan non-linear antara variabel. Misalnya, kita bisa menggunakan regresi polinomial untuk memprediksi pertumbuhan populasi suatu spesies berdasarkan waktu, karena pertumbuhan populasi bisa mengikuti pola non-linear.
Contoh Kasus: Seorang ahli pertanian ingin memprediksi hasil panen berdasarkan jumlah pupuk yang diberikan. Hubungan antara pupuk dan hasil panen mungkin tidak linear. Regresi polinomial dapat membantu mengidentifikasi pola non-linear ini dan memprediksi hasil panen dengan lebih akurat.
Asumsi Model Regresi Linear
Beberapa asumsi mendasari model regresi linear. Asumsi-asumsi ini penting untuk memastikan hasil analisis yang valid dan dapat diandalkan. Pelanggaran terhadap asumsi-asumsi ini dapat menghasilkan kesalahan dalam interpretasi hasil.
- Kenormalan Residu: Residu (selisih antara nilai aktual dan nilai prediksi) harus terdistribusi normal.
- Homoskedastisitas: Varians dari residu harus konstan untuk semua nilai variabel independen.
- Independensi Residu: Residu harus saling independen satu sama lain.
- Linearitas: Hubungan antara variabel independen dan dependen harus linear.
- Tidak adanya multikolinearitas (untuk regresi berganda): Variabel independen tidak boleh terlalu berkorelasi satu sama lain.
Dampak Pelanggaran Asumsi: Pelanggaran terhadap asumsi-asumsi ini dapat mengakibatkan:
- Penaksir yang tidak efisien: Koefisien regresi yang dihasilkan mungkin tidak akurat dan tidak efisien dalam memprediksi nilai.
- Ketidakpercayaan interval: Interval kepercayaan untuk koefisien regresi mungkin tidak akurat.
- Kesimpulan yang salah: Interpretasi hasil analisis mungkin tidak akurat atau salah.
Metode Estimasi Parameter

Metode estimasi parameter merupakan langkah krusial dalam analisis regresi linear. Proses ini bertujuan untuk menentukan nilai terbaik bagi parameter-parameter model, seperti koefisien regresi, yang dapat memaksimalkan kecocokan model dengan data yang diamati. Pemahaman yang baik tentang metode-metode ini penting untuk menginterpretasikan hasil analisis dan mengambil kesimpulan yang tepat.
Metode Kuadrat Terkecil
Metode kuadrat terkecil ( Ordinary Least Squares/OLS) adalah metode yang paling umum digunakan untuk mengestimasi parameter dalam regresi linear. Metode ini berusaha meminimalkan jumlah kuadrat dari selisih antara nilai aktual dan nilai prediksi model. Tujuannya adalah untuk mendapatkan garis regresi yang sedekat mungkin dengan semua titik data.
Rumus Koefisien Regresi
Untuk regresi linear sederhana (dengan satu variabel prediktor), rumus untuk menghitung koefisien regresi menggunakan metode kuadrat terkecil adalah sebagai berikut:
b1 = Σ[(x i
-x̄)(y i
-ȳ)] / Σ(x i
-x̄) 2b 0 = ȳ
-b 1x̄
Dimana:
- b 1 adalah koefisien regresi (slope)
- b 0 adalah intercept
- x i dan y i adalah nilai variabel prediktor dan respon untuk observasi ke-i
- x̄ adalah rata-rata variabel prediktor
- ȳ adalah rata-rata variabel respon
Perhitungan Intercept dan Slope
Untuk menghitung nilai intercept (b 0) dan slope (b 1) dalam regresi linear sederhana, kita perlu melakukan beberapa langkah:
- Menghitung rata-rata variabel prediktor (x̄) dan rata-rata variabel respon (ȳ).
- Menghitung selisih antara setiap nilai xi dengan rata-rata x̄ dan selisih antara setiap nilai y i dengan rata-rata ȳ.
- Mengalikan selisih-selisih tersebut dan menjumlahkannya (Σ[(x i
- x̄)(y i
- ȳ)]).
- Menghitung kuadrat selisih antara setiap nilai x i dengan rata-rata x̄ dan menjumlahkannya (Σ(x i – x̄) 2).
- Menggunakan rumus yang diberikan sebelumnya untuk menghitung b 1 (koefisien regresi).
- Menggunakan rumus yang diberikan sebelumnya untuk menghitung b 0 (intercept).
Contoh Perhitungan
Misalkan kita memiliki data berikut untuk regresi linear sederhana:
| x | y |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 5 |
Dengan menggunakan rumus dan langkah-langkah di atas, kita dapat menghitung b 1 dan b 0. Hasil perhitungan akan ditunjukkan secara rinci dalam tabel di bawah ini. (Perhitungan manual detail bisa cukup panjang dan dihilangkan untuk contoh ini)
Sebagai contoh hasil perhitungan akan menghasilkan: b 1 = 2 dan b 0 = 0. Ini berarti persamaan garis regresi adalah y = 2x + 0.
Interpretasi Hasil Regresi
Setelah melakukan analisis regresi linear, langkah penting berikutnya adalah menginterpretasikan hasilnya. Interpretasi ini membantu memahami hubungan antar variabel dan mengidentifikasi faktor-faktor yang berpengaruh. Pemahaman yang baik terhadap hasil regresi sangat krusial dalam pengambilan keputusan yang didasarkan pada model tersebut.
Interpretasi Koefisien Regresi
Koefisien regresi menunjukkan pengaruh variabel independen terhadap variabel dependen. Nilai koefisien regresi mengindikasikan besarnya perubahan variabel dependen untuk setiap satu unit perubahan variabel independen, dengan asumsi variabel lain tetap konstan. Koefisien positif menunjukkan hubungan linier positif, sementara koefisien negatif menunjukkan hubungan linier negatif.
Contohnya, jika koefisien regresi untuk variabel “pengeluaran iklan” adalah 2,5, ini berarti setiap penambahan Rp 1.000.000 pada pengeluaran iklan diperkirakan akan meningkatkan penjualan sebesar Rp 2.500.000, dengan asumsi variabel lain seperti harga dan persaingan tetap sama.
Interpretasi Nilai R-squared
Nilai R-squared (koefisien determinasi) mengukur seberapa baik model regresi menjelaskan variasi dalam data. Nilai R-squared berkisar antara 0 dan 1. Nilai yang mendekati 1 menunjukkan model yang lebih baik dalam menjelaskan variasi data. Nilai yang rendah mengindikasikan model kurang baik dalam menjelaskan variasi.
Misalnya, jika R-squared sebesar 0,85, maka model regresi tersebut dapat menjelaskan 85% variasi dalam data variabel dependen. Sisanya 15% dipengaruhi oleh faktor lain yang tidak dimasukkan dalam model.
Signifikansi Statistik Koefisien Regresi
Signifikansi statistik koefisien regresi diukur dengan nilai p-value. Nilai p-value yang kecil (biasanya di bawah 0,05) mengindikasikan bahwa koefisien regresi signifikan secara statistik. Artinya, perubahan pada variabel independen memang berpengaruh terhadap variabel dependen, bukan hanya kebetulan.
Jika p-value tinggi, maka koefisien regresi tidak signifikan secara statistik. Hal ini berarti perubahan pada variabel independen tidak berpengaruh signifikan terhadap variabel dependen. Koefisien tersebut sebaiknya dipertimbangkan kembali untuk dimasukkan dalam model.
Contoh Interpretasi Hasil Regresi
Misalkan kita ingin memprediksi penjualan berdasarkan pengeluaran iklan dan harga produk. Berikut contoh hasil regresi:
| Variabel | Koefisien | Nilai p-value |
|---|---|---|
| Pengeluaran Iklan | 2.5 | 0.001 |
| Harga Produk | -1.2 | 0.03 |
| Konstanta | 100 | 0.0001 |
Dari hasil tersebut, pengeluaran iklan (koefisien 2.5, p-value 0.001) dan harga produk (koefisien -1.2, p-value 0.03) berpengaruh signifikan terhadap penjualan. Semakin besar pengeluaran iklan, penjualan cenderung meningkat. Semakin tinggi harga produk, penjualan cenderung menurun. Konstanta (100) merepresentasikan penjualan saat pengeluaran iklan dan harga produk sama dengan nol.
Implikasi Hasil Regresi Terhadap Pengambilan Keputusan
Hasil regresi dapat memberikan wawasan penting bagi pengambilan keputusan. Jika pengeluaran iklan berpengaruh signifikan dan positif terhadap penjualan, maka perusahaan dapat mengalokasikan lebih banyak anggaran untuk iklan. Sebaliknya, jika harga produk berpengaruh negatif dan signifikan, maka perusahaan perlu mempertimbangkan strategi penetapan harga yang lebih tepat. Pemahaman terhadap hubungan antar variabel akan membantu dalam pengambilan keputusan bisnis yang lebih efektif.
Aplikasi Regresi Linear
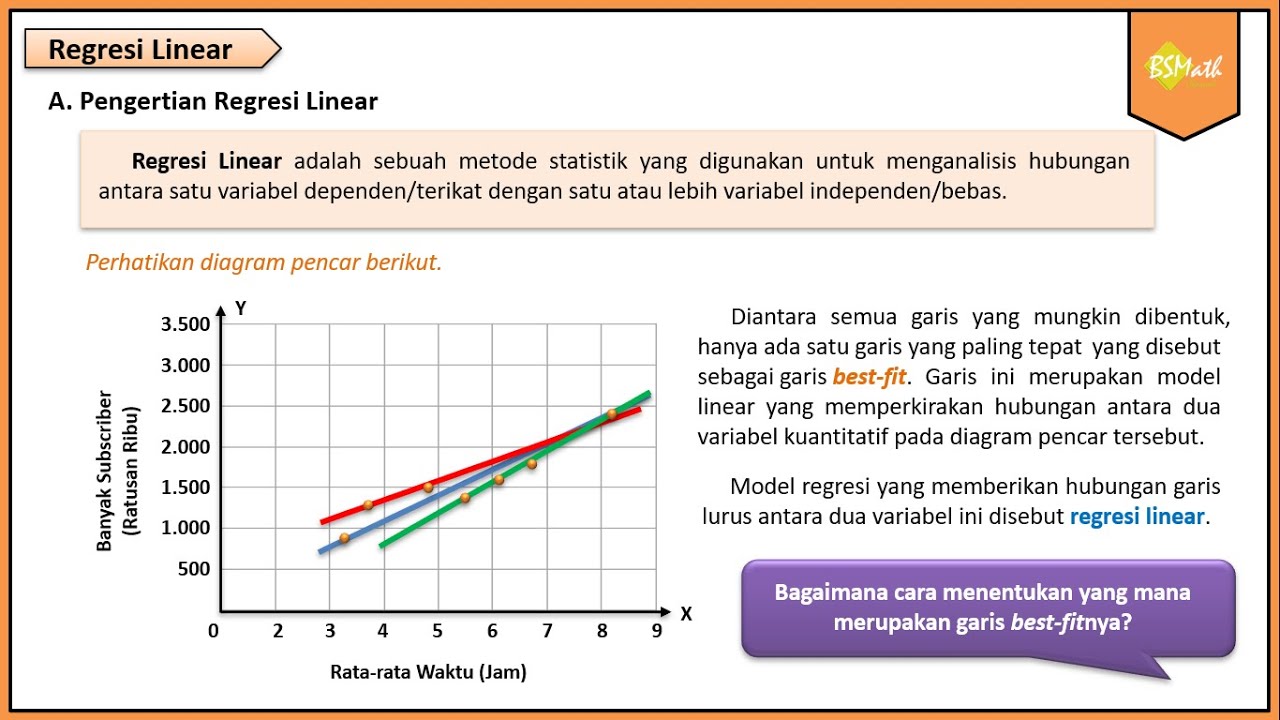
Regresi linear bukan sekadar teori matematika, tetapi memiliki beragam aplikasi praktis di berbagai bidang. Metode ini terbukti efektif dalam memodelkan hubungan antara variabel dan memprediksi nilai variabel tertentu. Pemahaman mendalam tentang penerapannya akan memberikan wawasan berharga dalam pengambilan keputusan dan pemahaman fenomena di berbagai sektor.
Penerapan Regresi Linear di Berbagai Bidang
Regresi linear dapat diterapkan di berbagai bidang, mulai dari ekonomi hingga ilmu sosial. Kemampuannya untuk memodelkan hubungan sebab-akibat menjadikannya alat yang berharga untuk analisis dan prediksi.
- Ekonomi: Memprediksi pertumbuhan ekonomi, menganalisis pengaruh suku bunga terhadap investasi, atau memprediksi permintaan pasar terhadap produk tertentu. Contohnya, regresi linear dapat digunakan untuk menganalisis hubungan antara pengeluaran iklan dan penjualan produk. Semakin tinggi pengeluaran iklan, semakin tinggi pula prediksi penjualan.
- Bisnis: Memprediksi penjualan berdasarkan faktor-faktor seperti iklan, promosi, dan tren pasar. Contoh lain, regresi linear dapat digunakan untuk menentukan harga produk berdasarkan biaya produksi, biaya pemasaran, dan faktor-faktor lain. Semakin tinggi biaya, semakin tinggi pula harga yang mungkin dipatok.
- Ilmu Sosial: Menganalisis hubungan antara pendidikan dan pendapatan, atau pengaruh tingkat pengangguran terhadap tingkat kejahatan. Misalnya, regresi linear dapat digunakan untuk menganalisis hubungan antara tingkat pendidikan dan penghasilan. Semakin tinggi tingkat pendidikan, semakin tinggi pula prediksi penghasilan.
Prediksi Nilai Variabel Dependen
Regresi linear memungkinkan kita untuk memprediksi nilai variabel dependen (variabel yang dipengaruhi) berdasarkan nilai variabel independen (variabel yang mempengaruhi). Prediksi ini didasarkan pada model hubungan yang telah dibangun.
Misalnya, dalam studi tentang pengaruh pengeluaran iklan pada penjualan, regresi linear dapat digunakan untuk memprediksi penjualan berdasarkan berbagai tingkat pengeluaran iklan. Model yang dihasilkan akan memperkirakan berapa banyak penjualan yang akan terjadi untuk setiap tingkat pengeluaran iklan yang berbeda.
Studi Kasus Nyata
Berikut contoh studi kasus sederhana. Seorang peneliti ingin mengetahui hubungan antara jam belajar dan nilai ujian matematika.
| Jam Belajar (X) | Nilai Ujian (Y) |
|---|---|
| 2 | 60 |
| 4 | 75 |
| 6 | 85 |
| 8 | 90 |
Dari data ini, regresi linear dapat membangun model yang menggambarkan hubungan linier antara jam belajar dan nilai ujian. Model ini kemudian dapat digunakan untuk memprediksi nilai ujian seseorang berdasarkan jam belajarnya. Visualisasi data ini dapat diilustrasikan dengan scatter plot yang menunjukkan titik-titik data dan garis regresi yang dihasilkan. Garis regresi ini merepresentasikan hubungan antara jam belajar dan nilai ujian.
Mengidentifikasi Hubungan Sebab-Akibat, Materi matematika regresi linear
Meskipun regresi linear dapat menunjukkan hubungan antara variabel, penting untuk diingat bahwa metode ini tidak selalu menunjukkan hubungan sebab-akibat. Korelasi tidak selalu sama dengan kausalitas. Faktor lain yang tidak terukur mungkin turut berperan dalam hubungan yang diamati. Analisis lebih lanjut dan pertimbangan faktor lain diperlukan untuk menyimpulkan hubungan sebab-akibat.
Contohnya, meskipun regresi linear dapat menunjukkan korelasi positif antara jumlah jam belajar dan nilai ujian, hal itu tidak secara otomatis berarti bahwa jam belajar
-menyebabkan* peningkatan nilai ujian. Faktor-faktor lain seperti motivasi, kemampuan kognitif, atau kualitas pengajaran dapat berperan juga.
Asumsi dan Diagnostik dalam Regresi Linear
Validitas model regresi linear sangat bergantung pada asumsi-asumsi yang mendasarinya. Memahami dan mendeteksi pelanggaran terhadap asumsi-asumsi ini sangat penting untuk menghasilkan interpretasi yang tepat dan model yang akurat. Bagian ini akan membahas asumsi-asumsi kunci, metode deteksi, dan prosedur diagnostik untuk regresi linear.
Asumsi-Asumsi Regresi Linear
Untuk mendapatkan hasil yang valid, model regresi linear harus memenuhi beberapa asumsi penting. Berikut ini beberapa asumsi tersebut:
- Linearitas: Hubungan antara variabel dependen dan variabel independen bersifat linier.
- Independensi Residuals: Residuals (sisaan) dari model harus independen satu sama lain. Artinya, nilai residual satu pengamatan tidak boleh berkorelasi dengan nilai residual pengamatan lainnya.
- Homoskedastisitas: Varians dari residual konstan untuk semua nilai variabel independen. Hal ini berarti penyebaran residual relatif sama di seluruh rentang variabel independen.
- Normalitas Residuals: Residuals mengikuti distribusi normal.
- Tidak adanya Multikolinieritas: Variabel independen tidak berkorelasi sempurna satu sama lain.
Metode Deteksi Pelanggaran Asumsi
Berikut ini beberapa metode yang dapat digunakan untuk mendeteksi pelanggaran asumsi-asumsi tersebut:
- Plot Scatter: Plot scatter antara variabel dependen dan variabel independen dapat digunakan untuk mengevaluasi linearitas.
- Plot Residuals: Plot residual terhadap nilai prediksi dan variabel independen dapat membantu mendeteksi pelanggaran homoskedastisitas dan non-linearitas. Residuals yang menyebar acak dan tidak membentuk pola tertentu mengindikasikan homoskedastisitas.
- Durbin-Watson Test: Digunakan untuk mendeteksi autokorelasi pada residual.
- Histogram dan Q-Q Plot: Digunakan untuk mengevaluasi normalitas distribusi residual. Histogram yang mendekati distribusi normal dan Q-Q plot yang menunjukkan titik-titik berjajar di sepanjang garis diagonal mengindikasikan normalitas.
- Variance Inflation Factor (VIF): Digunakan untuk mendeteksi multikolinieritas. Nilai VIF yang tinggi (biasanya di atas 5 atau 10) mengindikasikan adanya multikolinieritas.
Tabel Ringkasan Asumsi dan Deteksi Pelanggaran
| Asumsi | Penjelasan | Metode Deteksi |
|---|---|---|
| Linearitas | Hubungan linier antara variabel dependen dan independen. | Plot scatter, plot residual vs prediksi |
| Independensi Residuals | Residuals tidak berkorelasi. | Durbin-Watson test, plot residual vs urutan pengamatan |
| Homoskedastisitas | Varians residual konstan. | Plot residual vs prediksi, plot residual vs variabel independen |
| Normalitas Residuals | Residuals berdistribusi normal. | Histogram, Q-Q plot |
| Tidak ada Multikolinieritas | Variabel independen tidak berkorelasi sempurna. | Variance Inflation Factor (VIF) |
Prosedur Diagnostik
Berikut langkah-langkah dalam prosedur diagnostik untuk model regresi linear:
- Evaluasi plot scatter antara variabel dependen dan independen untuk memeriksa linearitas.
- Lakukan uji Durbin-Watson untuk mendeteksi autokorelasi.
- Buat plot residual terhadap nilai prediksi dan variabel independen untuk mengevaluasi homoskedastisitas.
- Buat histogram dan Q-Q plot untuk mengevaluasi normalitas residual.
- Hitung VIF untuk mendeteksi multikolinieritas.
- Jika terdapat pelanggaran asumsi, lakukan transformasi data atau metode lain untuk memperbaiki model.
Contoh Visualisasi Pelanggaran Asumsi
Contoh visualisasi pelanggaran asumsi (di sini perlu contoh grafik/visualisasi data yang menunjukkan pelanggaran linearitas, heteroskedastisitas, dan sebagainya). Grafik-grafik ini akan memperlihatkan pola-pola yang tidak diinginkan pada data, seperti penyebaran residual yang tidak merata atau hubungan non-linier.
Penutup
Kesimpulannya, regresi linear merupakan alat analisis data yang powerful untuk memahami hubungan antar variabel dan memprediksi nilai variabel dependen. Dengan pemahaman yang mendalam tentang konsep, metode, dan aplikasinya, kita dapat memanfaatkan regresi linear untuk menganalisis berbagai fenomena dan mengambil keputusan yang lebih informatif. Semoga materi ini dapat memberikan wawasan dan pemahaman yang komprehensif tentang regresi linear.